斐波那契数列
2014-05-29
主要是四种解法。
第一种:基本常用
公式:F(n) = F(n-1) + F(n-2)
function fib1(n)
if n = 0: return 0
if n = 1: return 1
return fib1(n-1) + fib1(n-2)
这种方法效率不高,基本是指数级别的。因为做了太多重复的计算操作。
第二种:保存中间结果(多项式级别)
function fib2(n)
if n = 0:return 0
int f[0...n] //保存中间结果的数组
f[0] = 0 f[1] = 1
for i = 2....n:
f[i] = f[i - 1]+f[i - 2]
return f[n]
该方法的效率是线性级别的。
第三种:利用矩阵乘法
等式F1 = F1和F2 = F0 + F1对应于以下矩阵运算:
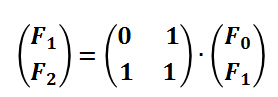
同样的有:
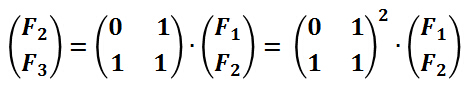
以及一般式:
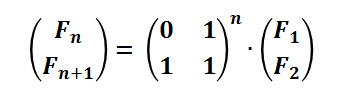
第四种:公式
计算斐波那契数列的公式: